Tensorflow vs Keras

TLDR: if you want to use deep learning as a tool, you should probably use Keras. If you're researching deep learning itself, you might need the fine grained control of TensorFlow.

Recently I’ve had some ideas for deep learning projects, and wanted to use Python to do it because it’s great for rapid prototyping and I’m comfortable with some great relevant libraries like numpy, pandas and Pillow. I like Torch7, but am just not as confident in Lua and would miss those tools. TensorFlow has a lot of momentum, but has a rather high barrier to entry. What Keras does is provide a high-level interface on top of TensorFlow. It also lets you use Theano as a back end, but we wont go in to that here.

I’m comparing Tensorflow against Keras instead of similar projects like TFLearn, TFSlim, or another TFLearn, mainly because Keras seems to be the most established in terms of buzz I’ve heard online, the amount of work done on each of those Github repos, and it felt like a general Keras-consensus on this Reddit thread. NB: that thread suggests Keras may be somewhat slower than pure Tensorflow. However, for the sake of my projects rapid prototyping is initially more valuable than rapid training. Lets see if I live to regret that statement.

All the code is available in this Jupyter notebook.

The Task

I’d like to experiment with a few methods for using neural networks for sorting arrays. I’m curious how they can do, and it’s going to be crazy easy to get loads of training data. We'll use a dead simple 1 layer network (OK, this isn't really deep learning), and array of length 2 which should be pretty easy to sort.

Here’s how we get data in numpy (after some boring imports):

import seaborn as sns

def get_batch(array_size, n_samples=100):
    x = np.random.rand(n_samples, array_size)
    y = x.argsort()
    return x, y

I’m choosing to try and get the network to predict the results of an argsort here: the indices needed to sort the initial array. My thinking here is I can just then round the end result and use them for sorting my array, and end up with identical outputs instead of the network being penalised for not reproducing the inputs exactly in order. This certainly bears some testing, but not for the sake of this post. It also enables a neat evaluation function, which you can interpret as 'percent of order integers that were correct':

def evaluate(y_pred, y_actual):
    score = np.mean(y_pred.round() == y_actual)*100
    return score

Before we get any further, lets also define some hyperparameters we'll use in all the tests.

array_size = 2 # How long the arrays are we'll sort. Not very long at all.
runs = 500 # Number of training runs
batch_size=10000 # Number of training examples in each training run

Code

Defining the models

import tensorflow as tf
sess = tf.InteractiveSession()

# Placeholder variables for the inputs and outputs
x = tf.placeholder(tf.float32, shape=[None, array_size])
y_ = tf.placeholder(tf.float32, shape=[None, array_size])

# Set up the variables for our fully connected layer
W = tf.Variable(tf.zeros([array_size, array_size]))
b = tf.Variable(tf.zeros([array_size]))

# Implement our fully connected layer
y = tf.matmul(x,W) + b

import keras

# Initiate our model

model = keras.models.Sequential()

# Add the layers

layer = keras.layers.Dense(
output_dim=array_size,
input_dim=array_size)
model.add(layer)

Tensorflow

import tensorflow as tf
sess = tf.InteractiveSession()

# Placeholder variables for the inputs and outputs

shape = [None, array_size]
x = tf.placeholder(tf.float32, shape=shape)
y\_ = tf.placeholder(tf.float32, shape=shape)

# Set up the variables for our fully connected layer

W = tf.Variable(tf.zeros([array_size, array_size]))
b = tf.Variable(tf.zeros([array_size]))

# Implement our fully connected layer

y = tf.matmul(x,W) + b

Keras

import keras

# Initiate our model
model = keras.models.Sequential()

# Add the layers
layer = keras.layers.Dense(
    output_dim=array_size,
    input_dim=array_size)
model.add(layer)

Tensorflow

import tensorflow as tf
sess = tf.InteractiveSession()

# Placeholder variables for the inputs and outputs
x = tf.placeholder(tf.float32, shape=[None, array_size])
y_ = tf.placeholder(tf.float32, shape=[None, array_size])

# Set up the variables for our fully connected layer
W = tf.Variable(tf.zeros([array_size, array_size]))
b = tf.Variable(tf.zeros([array_size]))

# Implement our fully connected layer
y = tf.matmul(x,W) + b

Keras

import keras

# Initiate our model
model = keras.models.Sequential()

# Add the layers
layer = keras.layers.Dense(output_dim=array_size, input_dim=array_size)
model.add(layer)

So:

• TensorFlow has the concept of a 'session', where our variables are instantiated, separate from our model.
• TensorFlow requires you to basically write out the maths behind a fully connected layer.

For me, I've pretty much found a winner at this point. The level of abstraction Keras offers is far more pleasant and quick to work with.

Defining the loss and optimisation functions

Tensorflow

# We're going to use mean squared error
error = tf.reduce_mean(tf.square(tf.sub(y_, y)))

# Our optimizer
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(error)

# Initialize all our variables
sess.run(tf.global_variables_initializer())

Keras

sgd = keras.optimizers.SGD(lr=0.5)
model.compile(loss='mse', optimizer=sgd)

In Tensorflow, again, we have to write out all the maths for mean squared error using their functions. Again, I found this much easier in Keras.

We also initialize both models here - model.compile does this in Keras behind the scenes.

Training

Tensorflow

losses = []
for i in range(runs):
    x_train, y_train = get_batch(array_size, batch_size)
    _, loss_val = sess.run([train_step, error],
                           feed_dict={x: x_train, y_:y_train})
    losses.append(loss_val)

Keras

losses = []
for i in range(runs):
    x_train, y_train = get_batch(array_size, batch_size)
    loss = model.train_on_batch(x_train, y_train)
    losses.append(loss)

The code length here is about the same. Things to note with TF: you run training in the session, and have to define 'fetches' - the graph elements you want to evaluate and return - as the first argument.

Code conclusion

For me this a hands-down win for Keras. Most people writing networks just wont need the control TensorFlow gives you, and the level of control comes at the high price of not giving you tools you'll want out of the box (fully connected layers, various error functions).

Aside validation

To boost my confidence they're doing the same thing, I plotted the learning rate over time of both with a large batch size.

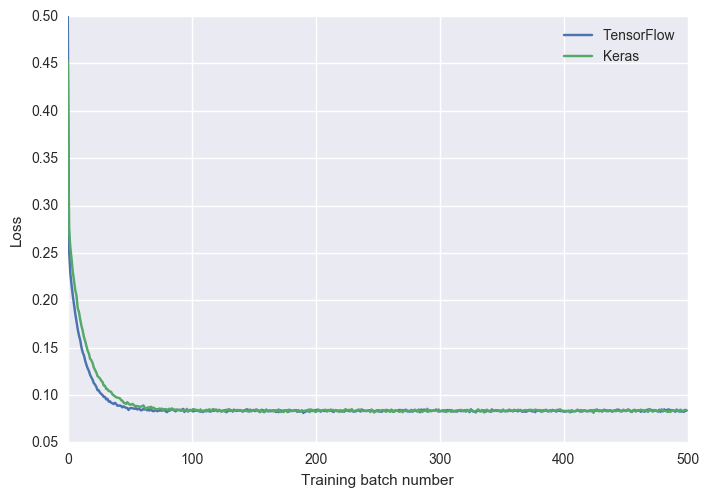
The initially faster learning for TensorFlow was consistent, but they end up in exactly the same place every time. They also scored very similarly on the evaluation function (both above 99% on several runs).

Speed

While I still maintain this is secondary, it's easy and interesting to do a benchmark. This isn't a great benchmark, as the network is so simple, but I'm curious to have an indication. So, the time it takes each to train each using ipythons %timeit:

• TensorFlow: 1.42s
• Keras: 1.45s

Pretty neck and neck. I ran it a few times and the results varied a lot, but I don't think there's anything in it. However, this found TensorFlow much (2x) faster and looks like a more real world test - I'd be slightly inclined to trust that more. But 2x isn't too bad for me.

Conclusion

I'll start learning Keras properly - the API was way faster and easier to develop with for this test case. Check out the code in notebook, looking at both all the way through makes you appreciate the simplicity even more.

Comment below if you have any thoughts, questions, or strong opinions on DL frameworks!